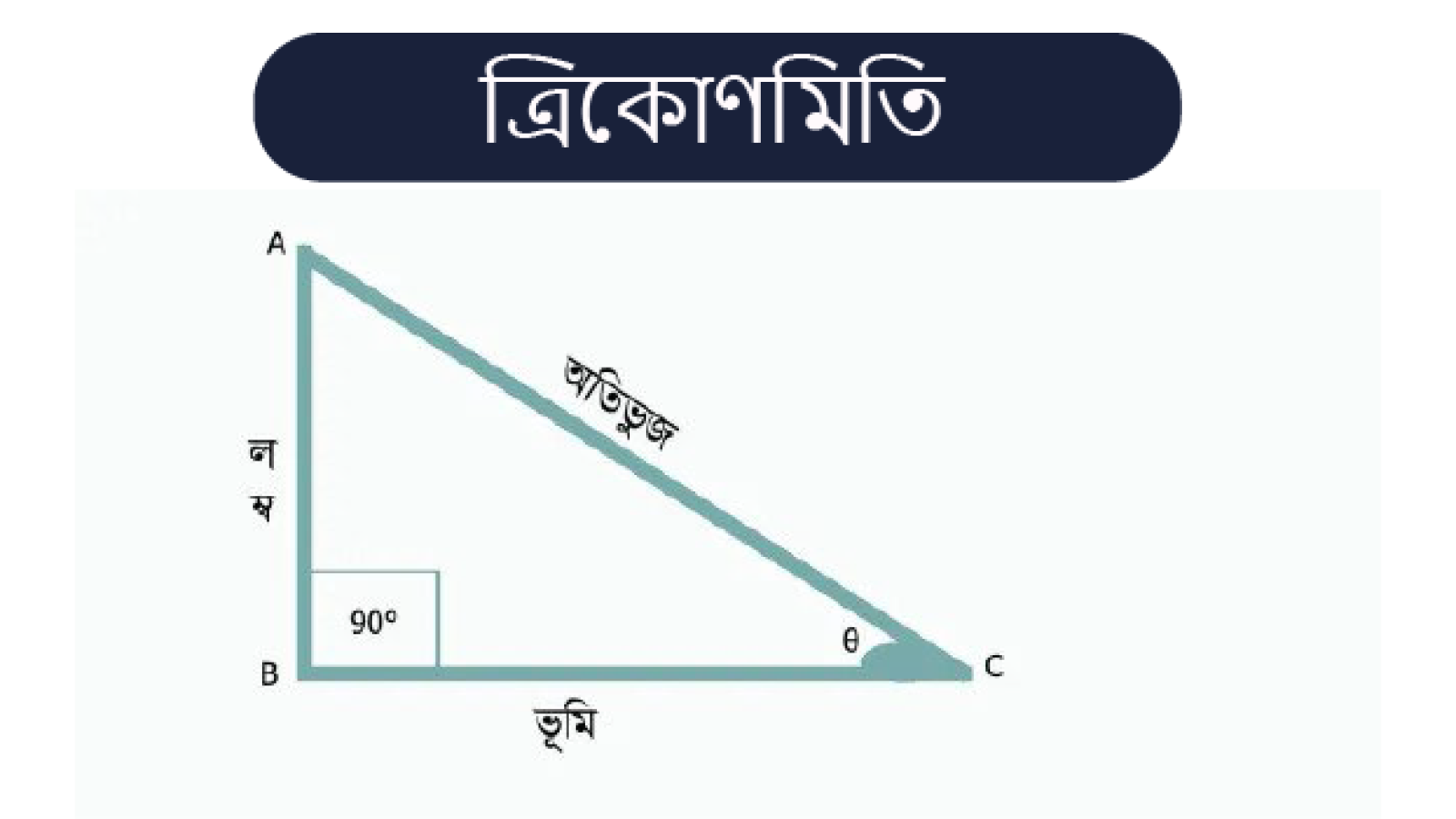
ত্রিকোণমিতি, কোণের নির্দিষ্ট ফাংশন এবং গণনায় তাদের প্রয়োগের সাথে সম্পর্কিত গণিতের শাখা। ত্রিকোণমিতিতে সাধারণত ব্যবহৃত একটি কোণের ছয়টি ফাংশন রয়েছে। তাদের নাম এবং সংক্ষিপ্ত রূপ হল sine (sin), cosine (cos), tangent (tan), cotangent (cot), secant (sec), এবং cosecant (csc)।
ত্রিকোণমিতি জ্যোতির্বিদ্যা, মানচিত্র তৈরি, জরিপ এবং আর্টিলারি রেঞ্জ অনুসন্ধানের মতো ক্ষেত্রে কোণ এবং দূরত্ব গণনা করার প্রয়োজন থেকে বিকশিত হয়েছে। একটি সমতলে কোণ এবং দূরত্ব জড়িত সমস্যা সমতল ত্রিকোণমিতিতে আচ্ছাদিত হয়। ত্রিমাত্রিক স্থানের একাধিক সমতলে অনুরূপ সমস্যার প্রয়োগগুলিকে গোলাকার ত্রিকোণমিতিতে বিবেচনা করা হয়।
ত্রিকোণমিতি শব্দটি এসেছে গ্রীক শব্দ trigonon (ত্রিভুজ) এবং মেট্রন (পরিমাপ করতে) থেকে। প্রায় 16 শতক পর্যন্ত, ত্রিকোণমিতি প্রধানত একটি ত্রিভুজের অনুপস্থিত অংশগুলির সংখ্যাসূচক মান গণনার সাথে সম্পর্কিত ছিল (বা ত্রিভুজগুলিতে বিচ্ছিন্ন করা যেতে পারে এমন কোনও আকৃতি) যখন অন্যান্য অংশগুলির মান দেওয়া হয়েছিল। উদাহরণস্বরূপ, যদি একটি ত্রিভুজের দুটি বাহুর দৈর্ঘ্য এবং আবদ্ধ কোণের পরিমাপ জানা যায়, তাহলে তৃতীয় বাহু এবং দুটি অবশিষ্ট কোণ গণনা করা যেতে পারে। এই ধরনের গণনাগুলি জ্যামিতি থেকে ত্রিকোণমিতিকে আলাদা করে, যা প্রধানত গুণগত সম্পর্কগুলি তদন্ত করে। অবশ্যই, এই পার্থক্যটি সর্বদা নিখুঁত নয়: উদাহরণস্বরূপ, পিথাগোরিয়ান উপপাদ্যটি একটি সমকোণী ত্রিভুজের তিনটি বাহুর দৈর্ঘ্য সম্পর্কে একটি বিবৃতি এবং তাই প্রকৃতিতে পরিমাণগত। তারপরও, তার আসল আকারে, ত্রিকোণমিতি ছিল জ্যামিতির একটি বংশধর; ষোড়শ শতাব্দী পর্যন্ত দুটি গণিতের পৃথক শাখায় পরিণত হয়নি।

বেশ কিছু প্রাচীন সভ্যতা – বিশেষ করে, মিশরীয়, ব্যাবিলনীয়, হিন্দু এবং চীনা- ব্যবহারিক জ্যামিতির যথেষ্ট জ্ঞানের অধিকারী ছিল, যার মধ্যে কিছু ধারণা ছিল যেগুলি ত্রিকোণমিতির একটি ভূমিকা ছিল। Rhind papyrus, প্রায় 1800 BCE থেকে পাটিগণিত, বীজগণিত এবং জ্যামিতির 84টি সমস্যার একটি মিশরীয় সংকলন, এতে সেকেডের সাথে মোকাবিলা করা পাঁচটি সমস্যা রয়েছে। পাঠ্যটির একটি ঘনিষ্ঠ বিশ্লেষণ, এর সহগামী পরিসংখ্যান সহ, প্রকাশ করে যে এই শব্দের অর্থ হল একটি ঝোঁকের ঢাল—পিরামিডের মতো বিশাল নির্মাণ প্রকল্পের জন্য প্রয়োজনীয় জ্ঞান। উদাহরণস্বরূপ, সমস্যা 56 জিজ্ঞাসা করে ;যদি একটি পিরামিড 250 হাত উঁচু হয় এবং এর ভিত্তির দিকটি 360 হাত লম্বা হয়, তাহলে এটির সন্ধান কী? দ্রবণটি প্রতি হাত 51/25 খেজুর হিসাবে দেওয়া হয়, এবং যেহেতু এক হাত 7 পামের সমান, এই ভগ্নাংশটি বিশুদ্ধ অনুপাত 18/25 এর সমতুল্য। এটি আসলে প্রশ্নে থাকা পিরামিডের রান-টু-রাইট অনুপাত – কার্যত, ভিত্তি এবং মুখের মধ্যে কোটের কোট্যানজেন্ট। এটি দেখায় যে মিশরীয়দের একটি ত্রিভুজের সংখ্যাগত সম্পর্ক সম্পর্কে অন্তত কিছু জ্ঞান ছিল, এক ধরণের প্রোটো-ত্রিকোণমিতি।
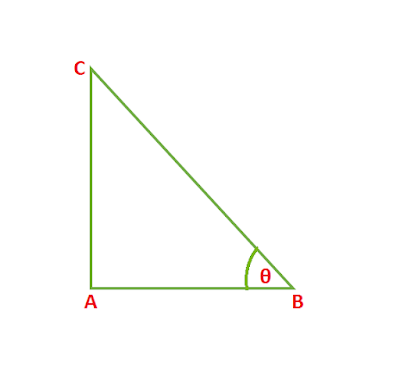
আধুনিক অর্থে ত্রিকোণমিতির সূচনা হয়েছিল গ্রিকদের মাধ্যমে। হিপারকাস (সি. 190-120 খ্রিস্টপূর্বাব্দ) ত্রিকোণমিতিক ফাংশনের জন্য মানগুলির একটি টেবিল তৈরি করেছিলেন। তিনি প্রতিটি ত্রিভুজ-প্লানার বা গোলাকার-কে একটি বৃত্তে খোদাই করা হিসাবে বিবেচনা করেছিলেন, যাতে প্রতিটি পাশে একটি জ্যা হয়ে যায় (অর্থাৎ, একটি সরল রেখা যা একটি বক্ররেখা বা পৃষ্ঠের দুটি বিন্দুকে সংযুক্ত করে, যেমনটি চিত্রে খোদাই করা ত্রিভুজ ABC দ্বারা দেখানো হয়েছে।) ত্রিভুজের বিভিন্ন অংশ গণনা করার জন্য, একজনকে কেন্দ্রীয় কোণের একটি ফাংশন হিসাবে প্রতিটি জ্যার দৈর্ঘ্য খুঁজে বের করতে হবে যা একে সাবটেন করে—অথবা, সমতুল্যভাবে, সংশ্লিষ্ট চাপের প্রস্থের ফাংশন হিসাবে একটি জ্যার দৈর্ঘ্য। এটি পরবর্তী কয়েক শতাব্দীর জন্য ত্রিকোণমিতির প্রধান কাজ হয়ে ওঠে। একজন জ্যোতির্বিজ্ঞানী হিসাবে, হিপারকাস মূলত গোলাকার ত্রিভুজগুলিতে আগ্রহী ছিলেন, যেমন মহাকাশীয় গোলকের তিনটি তারা দ্বারা গঠিত কাল্পনিক ত্রিভুজ, তবে তিনি সমতল ত্রিকোণমিতির মৌলিক সূত্রগুলির সাথেও পরিচিত ছিলেন। হিপারকাসের সময়ে এই সূত্রগুলিকে সম্পূর্ণরূপে জ্যামিতিক ভাষায় প্রকাশ করা হয়েছিল বিভিন্ন জ্যা এবং কোণগুলির (বা আর্কস) মধ্যে সম্পর্ক হিসাবে যা তাদের সাবটেন করে; ত্রিকোণমিতিক ফাংশনের জন্য আধুনিক চিহ্নগুলি 17 শতক পর্যন্ত চালু হয়নি।
ত্রিকোণমিতির উপর
প্রথম প্রধান প্রাচীন কাজটি অন্ধকার যুগের পরে অক্ষত ইউরোপে পৌঁছেছিল টলেমি (আনুমানিক 100-170 সিই) এর আলমাজেস্ট। তিনি হেলেনিস্টিক বিশ্বের বুদ্ধিবৃত্তিক কেন্দ্র আলেকজান্দ্রিয়াতে বাস করতেন, কিন্তু তার সম্পর্কে অন্য কিছু জানা যায় না। যদিও টলেমি গণিত, ভূগোল এবং আলোকবিদ্যার উপর কাজ লিখেছিলেন, তিনি মূলত আলমাজেস্টের জন্য পরিচিত, জ্যোতির্বিজ্ঞানের উপর একটি 13-বইয়ের সংকলন যা মানবজাতির বিশ্ব চিত্রের ভিত্তি হয়ে ওঠে যতক্ষণ না নিকোলাস কোপার্নিকাসের সূর্যকেন্দ্রিক সিস্টেম টলেমির ভূকেন্দ্রিক সিস্টেমকে প্রতিস্থাপন করা শুরু করে। 16 শতকের মাঝামাঝি। এই বিশ্ব চিত্রটি বিকাশ করার জন্য – যার সারাংশ ছিল একটি স্থির পৃথিবী যার চারপাশে সূর্য, চাঁদ এবং পাঁচটি পরিচিত গ্রহ বৃত্তাকার কক্ষপথে চলে – টলেমিকে কিছু প্রাথমিক ত্রিকোণমিতি ব্যবহার করতে হয়েছিল। আলমাজেস্টের প্রথম বইয়ের অধ্যায় 10 এবং 11 জ্যাগুলির একটি সারণী নির্মাণের সাথে সম্পর্কিত, যেখানে একটি বৃত্তে একটি জ্যার দৈর্ঘ্য কেন্দ্রীয় কোণের একটি ফাংশন হিসাবে দেওয়া হয় যা এটিকে সাবটেন করে, 0° থেকে কোণগুলির জন্য এক-অর্ধ ডিগ্রি ব্যবধানে 180° পর্যন্ত। এটি মূলত সাইনের একটি সারণী, যা c = 2r sin A/2 পেতে ব্যাসার্ধ r, চাপ A, এবং সাবটেন্ডেড জ্যা c এর দৈর্ঘ্য নির্দেশ করে দেখা যায়। যেহেতু টলেমি ব্যাবিলনীয় সেক্সজেসিমাল সংখ্যা এবং সংখ্যা পদ্ধতি (বেস 60) ব্যবহার করেছিলেন, তিনি r = 60 এককের ব্যাসার্ধের একটি আদর্শ বৃত্তের সাথে তার গণনা করেছিলেন, যাতে c = 120 sin A/2 হয়। এইভাবে, আনুপাতিকতা ফ্যাক্টর 120 ব্যতীত, তার ছিল sin A/2 এর মানগুলির একটি সারণী এবং তাই (চাপ দ্বিগুণ করে) sin A এর। তার টেবিলের সাহায্যে টলেমি বিশ্বের বিদ্যমান জিওডেটিক পরিমাপের উন্নতি করেছিলেন এবং হিপারকাসের পরিমার্জন করেছিলেন। স্বর্গীয় সংস্থার গতির মডেল।
ত্রিকোণমিতির পরবর্তী প্রধান অবদান ভারত থেকে এসেছে। সেক্সজেসিমাল পদ্ধতিতে, 120 (দুইবার 60) দ্বারা গুণ বা ভাগ করা হয় দশমিক পদ্ধতিতে 20 (দুইবার 10) দ্বারা গুণ বা ভাগের সাথে সাদৃশ্যপূর্ণ। এইভাবে, টলেমির সূত্রটিকে c/120 = sin B হিসাবে পুনঃলিখন, যেখানে B=A/2, সম্পর্কটি অর্ধ-জ্যাকে আর্ক B এর ফাংশন হিসাবে প্রকাশ করে যা এটিকে সাবটেন করে — অবিকল আধুনিক সাইন ফাংশন। সাইনের প্রথম সারণীটি আর্যভটিয়ায় পাওয়া যায়। এর লেখক, আর্যভট্ট I (c. 475-550), অর্ধ-জ্যা-এর জন্য অর্ধ-জ্যা শব্দটি ব্যবহার করেছেন, যা তিনি মাঝে মাঝে জ্যা-অর্ধ (জ্যা-অর্ধ) তে ঘুরেছেন; যথাসময়ে তিনি এটিকে ছোট করে জ্যা বা জীব। পরে, যখন মুসলিম পণ্ডিতরা এই কাজটি আরবি ভাষায় অনুবাদ করেছিলেন, তখন তারা এর অর্থ অনুবাদ না করেই জীব শব্দটিকে ধরে রেখেছেন। সেমিটিক ভাষায় শব্দগুলি বেশিরভাগ ব্যঞ্জনবর্ণ নিয়ে গঠিত, অনুপস্থিত স্বরগুলির উচ্চারণ সাধারণ ব্যবহার দ্বারা বোঝা যায়। এইভাবে জিবাকে জিবা বা জাইব হিসাবেও উচ্চারণ করা যেতে পারে এবং আরবীতে এই শেষ শব্দটির অর্থ ভাঁজ । যখন আরব অনুবাদটি ল্যাটিন ভাষায় অনুবাদ করা হয়, তখন জাইব হয়ে ওঠে সাইনাস, বে-এর ল্যাটিন শব্দ। সাইনাস শব্দটি সর্বপ্রথম ক্রেমোনার ঘেরার্ডো (c. 1114-87) এর লেখায় আবির্ভূত হয়েছিল, যিনি আলমাজেস্ট সহ অনেক গ্রীক পাঠ্য ল্যাটিন ভাষায় অনুবাদ করেছিলেন। অন্যান্য লেখকরা অনুসরণ করেন এবং শীঘ্রই সাইনাস বা সাইন শব্দটি সমগ্র ইউরোপ জুড়ে গাণিতিক সাহিত্যে ব্যবহৃত হয়। সংক্ষিপ্ত চিহ্ন sin প্রথম 1624 সালে এডমন্ড গুন্টার, একজন ইংরেজ মন্ত্রী এবং যন্ত্র নির্মাতা দ্বারা ব্যবহার করা হয়েছিল। অবশিষ্ট পাঁচটি ত্রিকোণমিতিক ফাংশনের জন্য স্বরলিপি খুব শীঘ্রই চালু করা হয়েছিল।
রাবেয়া আলম
ইন্সট্রাক্টর